728x90
반응형
1. 문제
https://www.acmicpc.net/problem/9527
9527번: 1의 개수 세기
두 자연수 A, B가 주어졌을 때, A ≤ x ≤ B를 만족하는 모든 x에 대해 x를 이진수로 표현했을 때 1의 개수의 합을 구하는 프로그램을 작성하시오. 즉, f(x) = x를 이진수로 표현 했을 때 1의 개수라
www.acmicpc.net
2. 알고리즘 분류
- 수학
- 누적 합
- 비트마스킹
3. 소스 코드
#include <iostream>
#define MAX 55
using namespace std;
long long A, B;
long long power[MAX];
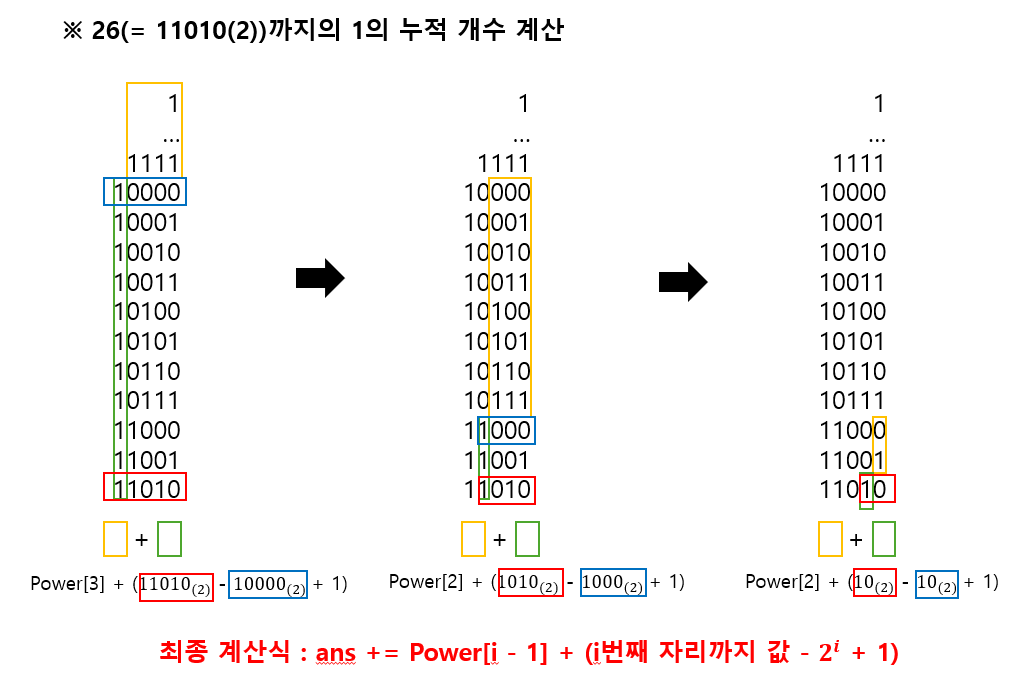
// 1 ~ x까지 모든 수의 1의 개수의 합 계산 함수
long long calculate(long long x)
{
long long ret = x & 1;
// 계산식 : ret += (최상위 비트가 i - 1번 이하인 누적 합) + (x - 2^i + 1)
for (int i = MAX - 1; i > 0; i--)
{
if (x & (1LL << i))
{
ret += power[i - 1] + (x - (1LL << i) + 1);
x -= 1LL << i;
}
}
return ret;
}
int main()
{
// I/O 속도 향상
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
// 누적 합 계산
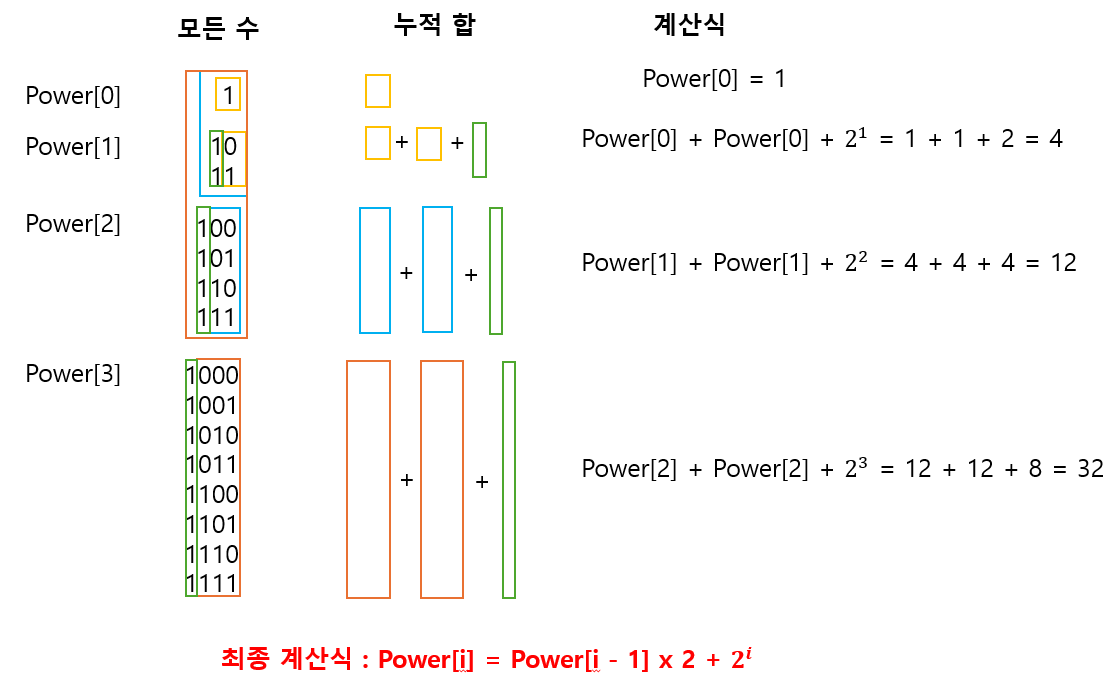
// power[i] = 최상위 비트가 i번 이하인 모든 수의 1의 개수의 합
// ex) power[2] = 1 ~ 111(2)까지 모든 수의 1의 개수의 합, power[5] = 1 ~ 11111(2)까지 모든 수의 1의 개수의 합
// 계산식 : power[i] = power[i - 1] * 2 + 2^i
power[0] = 1;
for (long long i = 1; i < 55; i++)
power[i] = power[i - 1] * 2 + (1LL << i);
// A, B : 자연수 입력
cin >> A >> B;
// 부분 합 계산
// A ~ B 까지 누적 합 = (1 ~ B까지 누적 합) - (1 ~ A - 1까지 누적 합)
// 예) 5 ~ 10까지 누적 합 = (1 ~ 10까지 누적 합) - (1 ~ 4까지 누적 합)
long long ans = calculate(B) - calculate(A - 1);
cout << ans;
return 0;
}
4. 유용한 알고리즘
1) 풀이 과정
728x90
'백준 알고리즘 > 백준 CLASS 5' 카테고리의 다른 글
| [백준 C++] 12015번: 가장 긴 증가하는 부분 수열 2 (0) | 2024.04.14 |
|---|---|
| [백준 C++] 10775번: 공항 (0) | 2024.04.14 |
| [백준 C++] 1766번: 문제집 (0) | 2024.04.11 |
| [백준 C++] 1202번: 보석 도둑 (0) | 2024.04.06 |
| [백준 C++] 20303번: 할로윈의 양아치 (1) | 2024.04.03 |



