1. Depth First Search (DFS, 깊이 우선 탐색)
1. 완전 탐색 알고리즘
- 모든 경우의 수를 탐색하는 알고리즘
2. 한 루트로 최대한 깊이 탐색하는 방식
- 트리나 그래프에서 한 루트로 쭉 탐색하다가 끝에 도달하면 다시 이전으로 돌아와서 다른 루트로 가는 방식
- 미로 찾기에서 한 방향으로 쭉 가다가 막히면, 다시 이전 분기점으로 돌아와서 다른 방향으로 가보면서 모든 루트를 탐색하는 방식
2. 장점
1) 저장 공간의 수요가 비교적 적다.
- 현 경로상의 노드들만 기억하면 되므로
2) 목표 노드가 깊은 단계에 있을 경우, 해를 빨리 구할 수 있다.
3. 단점
1) 해가 없는 경로에 깊이 빠질 가능성이 있다.
- 미리 지정한 임의의 깊이까지만 탐색하고 목표 노드를 발견하지 못했다면, 다른 경로를 따라 탐색하는 방식이 유용할 수 있다.
2) 얻어진 해가 최단 경로가 된다는 보장이 없다.
- 경로가 다수인 경우, 탐색한 거리가 최단 거리라고 보기는 힘들다.
4. 구현
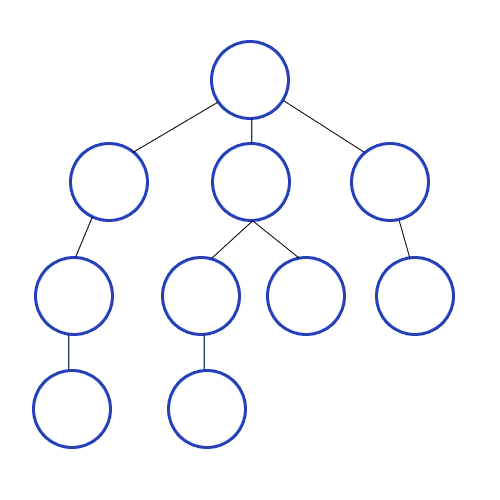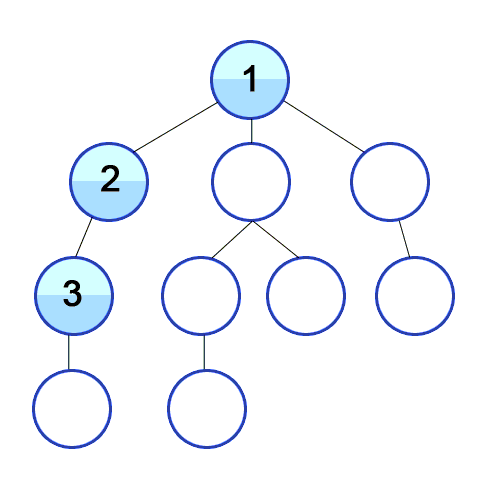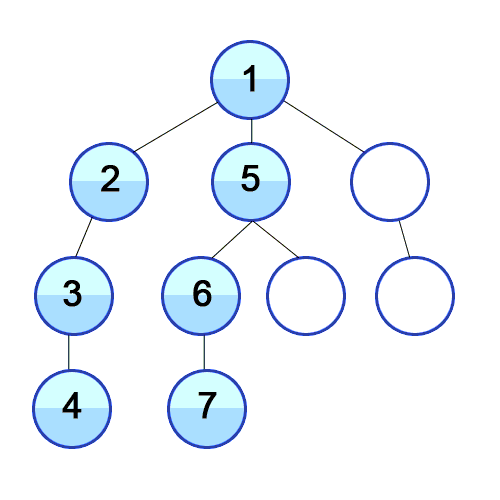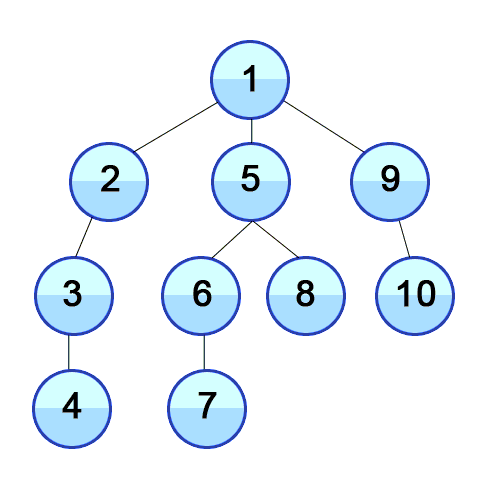
1) 재귀 방식
- 주로 사용하는 방식
#include <iostream>
#include <vector>
using namespace std;
bool visited[11];
vector<int> graph[11];
void dfs(int current_node)
{
visited[current_node] = true; // 방문 여부 체크
cout << current_node << " "; // 현재 노드 출력
for (int index = 0; index < graph[current_node].size(); index++)
{
int next_node = graph[current_node][index];
if (visited[next_node]) continue; // 방문한 노드라면 넘어가기
dfs(next_node); // 다음 노드 탐색
}
}
int main() {
// graph 생성
graph[1].push_back(2);
graph[1].push_back(5);
graph[1].push_back(9);
graph[2].push_back(3);
graph[3].push_back(4);
graph[5].push_back(6);
graph[5].push_back(8);
graph[6].push_back(7);
graph[9].push_back(10);
// DFS (깊이 우선 탐색) 알고리즘
dfs(1);
return 0;
}2) Stack 방식
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
bool visited[11];
vector<int> graph[11];
void dfs(int start_node)
{
stack<int> s;
s.push(start_node);
visited[start_node] = true;
cout << start_node << " ";
while(!s.empty())
{
int current_node = s.top();
s.pop();
for (int index = 0; index < graph[current_node].size(); index++) {
int next_node = graph[current_node][index];
if (visited[next_node]) continue;
cout << next_node << " ";
visited[next_node] = true;
s.push(current_node);
s.push(next_node);
break;
}
}
}
int main() {
// graph 생성
graph[1].push_back(2);
graph[1].push_back(5);
graph[1].push_back(9);
graph[2].push_back(3);
graph[3].push_back(4);
graph[5].push_back(6);
graph[5].push_back(8);
graph[6].push_back(7);
graph[9].push_back(10);
// DFS (깊이 우선 탐색) 알고리즘
dfs(1);
return 0;
}
5. 알고리즘 구조
아래 3가지 순서로 나눌 수 있다.
1) 방문 여부 체크
2) 기저 조건
3) 다음 노드 탐색
void dfs(int current_node)
{
// 1. 방문 여부 체크
visited[current_node] = true; // 방문 여부 체크
// 2. 기저 조건
if (current_node == 7) {
cout << "7번 문 탈출!!";
return;
}
// 3. 다음 노드 탐색
for (int index = 0; index < graph[current_node].size(); index++)
{
int next_node = graph[current_node][index];
if (visited[next_node]) continue; // 방문한 노드라면 넘어가기
dfs(next_node); // 다음 노드 탐색
}
}
6. DFS 문제 모음집
https://www.acmicpc.net/problem/16724
16724번: 피리 부는 사나이
첫 번째 줄에 지도의 행의 수를 나타내는 N(1 ≤ N ≤ 1,000)과 지도의 열의 수를 나타내는 M(1 ≤ M ≤ 1,000)이 주어진다. 두 번째 줄부터 N개의 줄에 지도의 정보를 나타내는 길이가 M인 문자열이 주
www.acmicpc.net
https://www.acmicpc.net/problem/9466
9466번: 텀 프로젝트
이번 가을학기에 '문제 해결' 강의를 신청한 학생들은 텀 프로젝트를 수행해야 한다. 프로젝트 팀원 수에는 제한이 없다. 심지어 모든 학생들이 동일한 팀의 팀원인 경우와 같이 한 팀만 있을
www.acmicpc.net
https://www.acmicpc.net/problem/2239
2239번: 스도쿠
스도쿠는 매우 간단한 숫자 퍼즐이다. 9×9 크기의 보드가 있을 때, 각 행과 각 열, 그리고 9개의 3×3 크기의 보드에 1부터 9까지의 숫자가 중복 없이 나타나도록 보드를 채우면 된다. 예를 들어 다
www.acmicpc.net
https://www.acmicpc.net/problem/1987
1987번: 알파벳
세로 $R$칸, 가로 $C$칸으로 된 표 모양의 보드가 있다. 보드의 각 칸에는 대문자 알파벳이 하나씩 적혀 있고, 좌측 상단 칸 ($1$행 $1$열) 에는 말이 놓여 있다. 말은 상하좌우로 인접한 네 칸 중의
www.acmicpc.net
https://www.acmicpc.net/problem/21736
21736번: 헌내기는 친구가 필요해
2020년에 입학한 헌내기 도연이가 있다. 도연이는 비대면 수업 때문에 학교에 가지 못해 학교에 아는 친구가 없었다. 드디어 대면 수업을 하게 된 도연이는 어서 캠퍼스 내의 사람들과 친해지고
www.acmicpc.net
https://www.acmicpc.net/problem/14502
14502번: 연구소
인체에 치명적인 바이러스를 연구하던 연구소에서 바이러스가 유출되었다. 다행히 바이러스는 아직 퍼지지 않았고, 바이러스의 확산을 막기 위해서 연구소에 벽을 세우려고 한다. 연구소는 크
www.acmicpc.net
https://www.acmicpc.net/problem/14888
14888번: 연산자 끼워넣기
첫째 줄에 수의 개수 N(2 ≤ N ≤ 11)가 주어진다. 둘째 줄에는 A1, A2, ..., AN이 주어진다. (1 ≤ Ai ≤ 100) 셋째 줄에는 합이 N-1인 4개의 정수가 주어지는데, 차례대로 덧셈(+)의 개수, 뺄셈(-)의 개수, 곱
www.acmicpc.net
https://www.acmicpc.net/problem/1799
'알고리즘' 카테고리의 다른 글
| [알고리즘] 그리디 알고리즘 (1) | 2024.04.06 |
|---|---|
| [알고리즘] BFS(너비 우선 탐색) (1) | 2024.04.03 |
| [알고리즘] 배낭 문제 (1) | 2024.04.03 |
| [기타] 주어진 수열에서 선택한 3개의 값의 합이 0에 가장 가깝게 선택하는 방법 (1) | 2023.10.03 |
| 투 포인터(Two Pointer) 알고리즘 (0) | 2023.10.03 |



