1. Segment Tree(세그먼트 트리)
Segment Tree(세그먼트 트리)는 배열 간격에 대한 정보를 이진 트리에 저장하는 자료구조입니다.
Segment Tree를 도식화하면, 아래와 같습니다.

Segment Tree는 다양한 활용법이 있겠지만, 특히 특정 데이터 배열의 구간 합을 계산할 때 유용합니다.
아래 예시를 통해, 단순 배열 방법과 Segment Tree 활용법을 비교해보겠습니다.
예시 1) 단순 배열 방법
array = {1, 2, 3, ..., N} 배열에서 특정 범위의 구간 합과 특정 인덱스의 값 변경을 M번 수행
(1) array 배열에서 1번째 ~ N번째까지 구간 합 연산
- S = array[0] + array[1] + array[2] + ... + array[N - 1]
- 시간 복잡도 : O(N)
- M번 연산시 시간 복잡도 : O(MN)
(2) i번째 배열 값을 a로 변경
- array[i] = a
- 시간 복잡도 : O(1)
- M번 연산시 시간 복잡도 : O(M)
(3) 특정 범위의 구간 합과 특정 인덱스의 값 변경을 M번 수행시, 총 시간 복잡도
- 총 시간 복잡도 : O(MN) + O(M) = O(MN)
예시 2) Segment Tree 활용법
(1) array 배열에서 1번째 ~ N번째까지 구간 합 연산
- 시간 복잡도 : O(logN)
- M번 연산시 시간 복잡도 : O(M logN)
(2) i번째 배열 값을 a로 변경
- 시간 복잡도 : O(logN)
- M번 연산시 시간 복잡도 : O(M logN)
(3) 특정 범위의 구간 합과 특정 인덱스의 값 변경을 M번 수행시, 총 시간 복잡도
- 총 시간 복잡도 : O(M logN) + O(M logN) = O(M logN)
최종적으로 단순 배열 방법과 Segment Tree 활용법을 비교하면 Segment Tree 활용법은 범위 최소/최대, 배열 구간 합 Query 및 Update 시간을 O(MN)에서 O(M logN)으로 개선할 수 있습니다.
2. Segment Tree 구조
Segment Tree는 이진 트리이며, 아래와 같이 도식화할 수 있습니다.

Segment Tree의 부모 노드와 자식 노드간의 인덱스 관계는 아래와 같습니다.
- 부모 노드의 인덱스 : i
- 자식 노드의 인덱스 : 2i / 2i + 1
또한, 각 노드마다 구간 정보와 구간 합 또는 구간 최대/최소 값의 정보를 저장하고 있습니다.
간단하게 정리하자면, 부모 노드에는 자식 노드들의 합이 저장되어 있습니다.
3. Segment Tree 구현
Segment Tree는 크게 Initial / Query / Update라는 3 가지 기능이 필요합니다. 3가지 기능을 알아보기 전에, 우선 세그먼트 트리를 생성할 때 필요한 노드 수를 계산해보겠습니다.
1) Segment Tree 노드 수
크기가 n개인 배열 기준으로 Segemnt Tree 생성시 필요한 노드 수는 아래와 같습니다.

Segment Tree의 높이는 h = [log2N]이며, 보통 편의상 필요한 배열 크기는 2^(h+1) 또는 4n으로 크기를 정합니다.
2) Segment Tree Initial(생성)
Segment Tree를 생성하는 함입니다. 편의상 Segment Tree 크기는 4n으로 정하겠습니다.
leaf node인 경우와 internal node인 경우로 나누어서 구현해야 합니다.
- leaf node (구간 범위의 크기가 1인 경우) : 해당 인덱스의 배열 값 저장
- internal node : 왼쪽 자식 노드와 오른쪽 자식 노드를 탐색하여 2개의 노드의 합을 저장
#define N 10
using namespace std;
int arr[N];
int segment_tree[4 * N];
int init(int node, int start, int end) {
// leaf Node인 경우
if (start == end) return segment_tree[node] = arr[start];
int mid = (start + end) / 2; // 중간 나누기
int left_child_node = node * 2;
int right_child_node = node * 2 + 1;
// 부모 노드 = 왼쪽 자식 노드 + 오른쪽 자식 노드
return segment_tree[node] = init(left_child_node, start, mid) + init(right_child_node, mid + 1, end);
}
3) Segment Tree Query(쿼리)
Segment Tree의 구간 정보를 가져오는 함수입니다.
Segment Tree를 순회하면서 아래 3가지 로직을 통해서 구간 정보를 취합합니다.
- 해당 노드의 범위가 지정된 범위 밖에 있다면, 0을 반환
- 해당 노드의 범위가 지정된 범위 내에 있다면, 해당 노드 값을 반환
- 해당 노드의 범위가 지정된 범위 일부만 포함한다면, 왼쪽 자식과 오른쪽 자식을 탐색하여 두 자식의 합을 반환
예를 들면 A = {1, 2, 3, 4, 5} 배열에서 2 ~ 4번째 구간 합을 구한다면, 아래 그럼처럼 컬러 노드들을 방문하게 되고, 그 중 초록색 노드 값들의 합을 반환하게 됩니다. (3 + 9 - 12)

#define N 10
using namespace std;
int arr[N];
int segment_tree[4 * N];
int query(int node, int start, int end, int left, int right) {
// 해당 노드의 범위가 지정된 범위를 벗어난 경우,
if (left > end || right < start) return 0;
// 해당 노드의 범위가 지정된 범위 내에 있는 경우,
if (left <= start && end <= right) return segment_tree[node];
// 해당 노드의 범위가 지정된 범위의 일부 포함한 경우,
int mid = (start + end) / 2;
int left_child_node = node * 2;
int right_child_node = node * 2 + 1;
return query(left_child_node, start, mid, left, right) + query(right_child_node, mid + 1, end, left, right);
}
4) Segment Tree Update
배열의 값이 변경되었을 때, Segment Tree도 변경하는 함수입니다.
변경된 인덱스와 관련된 노드와 변경합니다.
예를 들어, arr={1, 2, 3, 4, 5} 배열에서 arr[2] = 5로 변경할 때, 변경되는 구간은 아래와 같습니다.
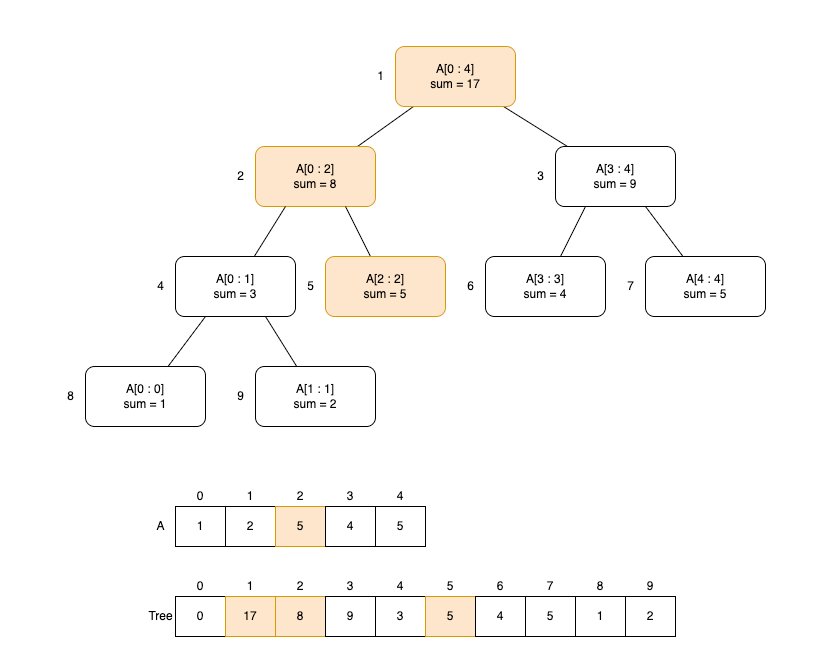
Segment Tree의 Update 기능은 2가지 방식으로 구현할 수 있습니다.
(1) 기존 방식
- leaf node에 도착한 경우, 해당 노드의 값을 변경
- internal node인 경우, 해당 인덱스 값이 왼쪽 자식 노드에 있으면 왼쪽 자식 노드 탐색, 오른쪽 자식 노드에 있으면 오른쪽 노드 탐색
#define N 10
using namespace std;
int arr[N];
int segment_tree[4 * N];
void update(int node, int start, int end, int index, int val) {
// leaf Node에 도착한 경우,
if (start == end) {
segment_tree[node] = val;
return;
}
int mid = (start + end) / 2;
int left_child_node = node * 2;
int right_child_node = node * 2 + 1;
if (start <= index && index <= mid) // 해당 인덱스가 왼쪽 자식에 있는 경우
update(left_child_node, start, mid, index, val);
else // 해당 인게스가 오른쪽 자식에 있는 경우
update(right_child_node, mid + 1, end, index, val);
// Segment Tree 값 갱신
// 부모 노드 = 왼쪽 자식 노드 + 오른쪽 자식 노드
segment_tree[node] = segment_tree[left_child_node] + segment_tree[right_child_node];
return;
}(2) 변화량을 사용한 방식
- 해당 인덱스가 노드 범위를 벗어난 경우, Segment Tree 갱신하지 않고 반환
- leaf node에 도착한 경우, Segment Tree 갱신 후 반환
- 자식 노드들 탐색
#define N 10
using namespace std;
int arr[N];
int segment_tree[4 * N];
void update(int node, int start, int end, int index, int diff) {
// 해당 인덱스가 노드 범위를 벗어난 경우
if (index < start || index > end) return;
// Segment Tree 갱신
segment_tree[node] += diff;
// leaf node에 도착한 경우,
if (start == end) return;
// 자식 노드 탐색
int mid = (start + end) / 2;
int left_child_node = node * 2;
int right_child_node = node * 2 + 1;
update(left_child_node, start, mid, index, diff);
update(right_child_node, mid + 1, end, index, diff);
}
4. Segment Tree 대표 문제
https://www.acmicpc.net/problem/2042
'알고리즘' 카테고리의 다른 글
| [알고리즘] 파스칼 삼각형을 활용한 조합 계산 (0) | 2024.09.05 |
|---|---|
| [알고리즘] 다이나믹 프로그래밍(DP, Dynamic Programming) (0) | 2024.05.04 |
| [알고리즘] CCW(Counter ClockWise) 기하 알고리즘 (0) | 2024.05.01 |
| [알고리즘] 이진 탐색(이분 탐색, Binary Search) (0) | 2024.04.14 |
| [알고리즘] 분리 집합(Union-Find) (0) | 2024.04.14 |



